

And now we've simplified the radical expression.

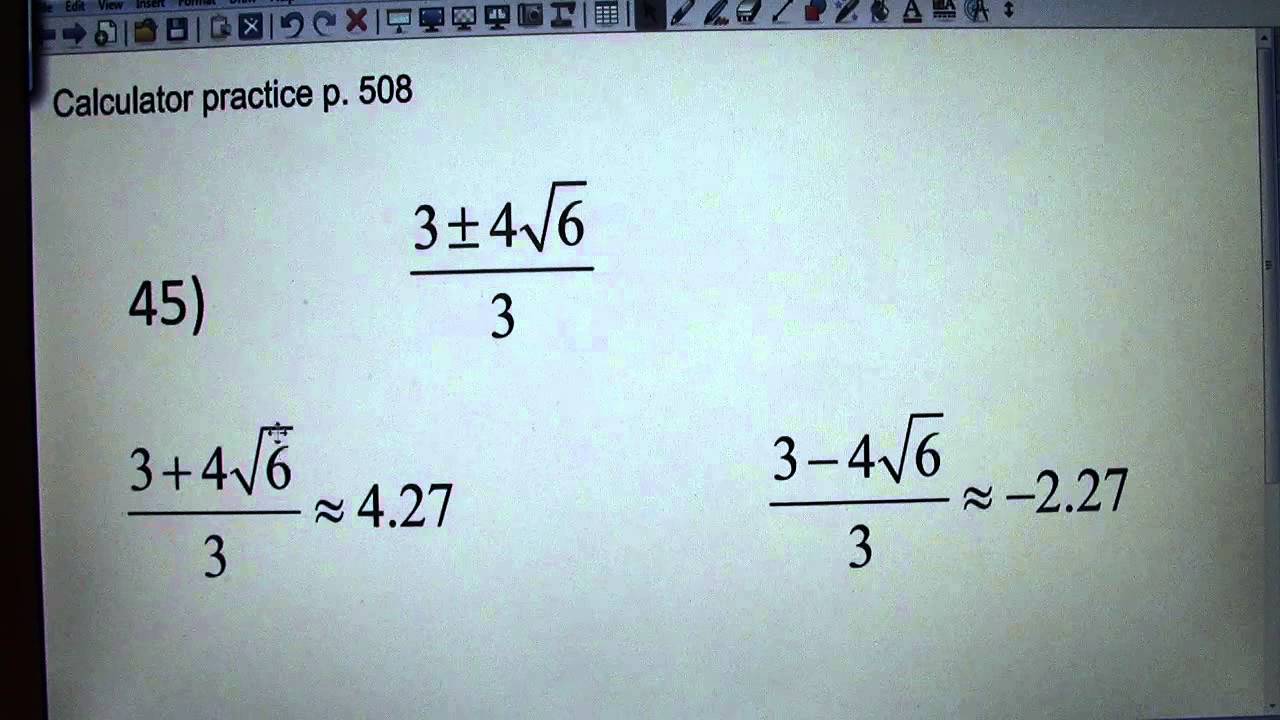
#Simplify radical expressions how to#
And now we've solved for it, and there's no way more to simplify, but this is an okay form to write this radical expression because there's no square root in the denominator, it's only in the numerator where it's allowed. How to Simplify Radicals Start by finding the prime factors of the number under the radical. Now split the original radical expression in the form of individual. Write down the numerical terms as a product of any perfect squares. If you have a term inside a square root the first thing you need to do is try to factorize it. So, we can by the rules of math multiply this by the square root of nine over the square root of nine, we get nine on the bottom, which is great, no more square root, and now we have five times the square root of nine on the top, which we just write as five root nine. In this video the instructor shows who to simplify radicals. Square root over nine over square root of nine is one, so we can multiply anything by one and it stays the same, it keeps its identity. But we can't just multiply the denominator by the square root of nine, we have to multiply the numerator by it as well so that we're actually really just multiplying this fraction by a version of one. If we multiply it by the square root of nine, the square root of nine from the square root of nine is nine, right? That's the square root of nine-squared, which is nine. So, what we do is multiply what we have in the denominator by itself to get rid of the square root. We give the Quotient Property of Radical Expressions again for easy reference. And it really just comes out of the exponent properties. The key to simplify this is to realize if I have the principal root of x over the principal root of y, this is the same thing as the principal root of x over y. We will need to use this property ‘in reverse’ to simplify a fraction with radicals. And we have one radical expression over another radical expression. For example, is considered simplified because there are no perfect square factors in 5. We cannot write this radical expression as such. We have used the Quotient Property of Radical Expressions to simplify roots of fractions. A radical expression, is considered simplified if it has no factors of So, to simplify a radical expression, we look for any factors in the radicand that are powers of the index. If we're given an example such as five over the square root of nine, we know that we can never have a square root in the denominator.
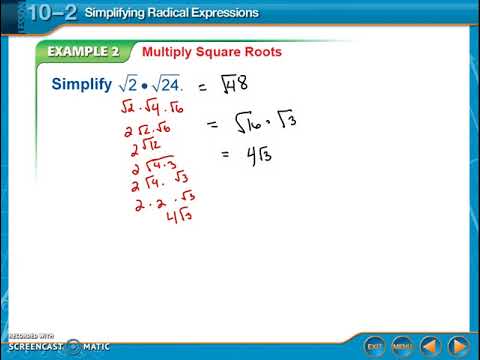
This process is called rationalizing the. Simplify radical expressions using factoring Simplify radical expressions using the product and quotient rule for radicals. An expression with a radical in its denominator should be simplified into one without a radical in its denominator.


 0 kommentar(er)
0 kommentar(er)
